Download PDF
Volumetric Positioning State (VPS / 5DVNS)
A Deterministic Framework for State-Based Positioning and Navigation
Prepared by: Hamdy Samy
Founder & IP Holder — 5DVNS
Date: February 2026
Executive Abstract
Positioning and navigation systems have historically been constructed around a single assumption: that
location is best represented as a point within an absolute reference frame. This assumption underlies global
navigation satellite systems (GNSS), inertial navigation systems (INS), simultaneous localization and
mapping (SLAM), and most contemporary autonomous navigation architectures.
This paper introduces a different premise.
Rather than treating position as a point in space, the Volumetric Positioning State (VPS / 5DVNS) models
position as a deterministic state embedded within a bounded volume, defined by geometric admissibility and
contextual integrity rather than absolute coordinates. Determinism is achieved by giving bounded uncertainty
sets and admissibility constraints. State validity evolves predictably without probabilistic correction
layers.
In this framework, position is not continuously corrected toward an external reference. Instead, positional
coherence is maintained through volumetric consistency under constraints. Guidance, stability, and
navigation outputs emerge from the persistence of admissible states over time.
The framework does not depend on privileged global reference frames, it does not require a persistent
global reference frame for state validity, it is robust to signal loss, vertical ambiguity, and map
unavailability. It reframes navigation from coordinate accuracy to state integrity, enabling coherent
operation across surface, subsurface, indoor, underwater, orbital, and non-physical domains.
This document formalizes the VPS state model, its invariance properties, and its interpretive shift,
without prescribing implementation details or domain-specific realizations.
1. Limits of Point-Based Positioning
Classical positioning systems represent location as a point:
P(t) = (x, y, z)
This formulation assumes:
- A stable external reference frame
- A privileged origin
- A continuous ability to correct drift
- A clear separation between position and uncertainty
While effective in open and well-instrumented environments, point-based positioning exhibits structural
fragility when:
- External references degrade or disappear
- Vertical ambiguity dominates (e.g., subsurface, indoor, underwater)
- Environments are dynamic, constrained, or unstructured
- Mapping is incomplete, outdated, or impossible
In such cases, systems compensate by layering probabilistic corrections, sensor fusion, or increasingly
complex maps—without addressing the underlying representational assumption.
The core limitation is not sensor quality or computation.
It is the choice of point as the primitive of
position.
2. From Coordinates to State Integrity
The VPS framework replaces point-based localization with state-based embedding.
Position is not asked as “Where am I?”
It is evaluated as “Is my current state
admissible within the volume I inhabit?”
Formally, position is expressed as:
S(t) = [x, y, d | V]
Where:
- x, y represent lateral embedding within a bounded manifold
- d represents scalar progression (depth, distance, phase, or corridor advancement)
- V is a volumetric context vector encoding: geometry, constraints, uncertainty,
stability, field or resonance behavior
The state is deterministic under bounded uncertainty.
Position emerges from volumetric consistency, not
absolute reference alignment.
In this model:
- Coordinates are observations, not authorities
- Sensors inform state evolution, but do not define position
- Drift is not eliminated, but made explicit and bounded
- Loss of external reference does not imply loss of coherence
Position becomes a property of state survivability under constraints over time.
3. Invariance Properties
The VPS formulation exhibits the following invariances:
- No dependence on fixed maps, magnetic north, or global orientation under constrained manifold embedding
- Robust to signal loss: coherence maintained without continuous external correction
- Robust to vertical ambiguity: depth and progression decoupled from Cartesian altitude
- Deterministic under bounded uncertainty: uncertainty is internalized, not externalized
- Domain-agnostic: applicable across surface, subsurface, indoor, underwater, orbital, and abstract
environments
These properties arise from the geometry of the state itself, not from redundancy or correction frequency.
4. Interpretive Shift
The framework introduces two fundamental transformations:
- From coordinate tracking → state integrity
- From position accuracy → positional confidence
Navigation guidance is not prescribed.
It emerges from the admissible evolution of states within
constraints.
This shifts navigation from optimization toward targets to maintenance of coherence.
Implementation Note
This document describes an operational-level construct.
Implementations may vary by domain, resolution, sensing modality, and risk profile. Certain structural
aspects of the framework are subject to prior art disclosures and active patent filings and are
intentionally described here at a conceptual level.
5. State Evolution and Admissibility
Within the VPS framework, navigation is the evolution of a state rather than the traversal of coordinates.
State evolution is governed by admissibility:
A state is valid if it remains geometrically and contextually consistent with the constraints encoded in V.
Formally, state transition does not seek an optimal target. It evaluates whether the next state remains
inside the admissible volume defined by:
- Geometric boundaries
- Environmental constraints
- Dynamic stability conditions
- Temporal progression limits
This introduces a critical distinction:
Trajectory is not planned in advance
Path viability is evaluated continuously
As long as the evolving state remains admissible, navigation proceeds. When admissibility degrades,
guidance emerges as a corrective signal—not toward a coordinate, but toward restored coherence.
In this sense, navigation is not command-driven.
It is constraint-driven.
6. Role of the Volumetric Context Vector (V)
The volumetric context vector V is not metadata.
It is a first-class component of the positional state. Unlike traditional systems where uncertainty,
constraints, or environmental factors are treated as error terms or auxiliary layers, VPS embeds them
directly into the state definition.
The vector V may encode, depending on domain and implementation:
- Geometric constraints (corridors, boundaries, exclusion zones)
- Stability margins (allowed deviation, tolerance envelopes)
- Uncertainty structure (bounded drift, sensor bias accumulation)
- Field behavior (electromagnetic, seismic, fluidic, or abstract fields)
- Resonance or persistence signatures
Crucially:
V does not describe the environment
V defines the conditions under which a state remains valid
This allows the system to reject impossible states deterministically, rather than correcting them
probabilistically after failure.
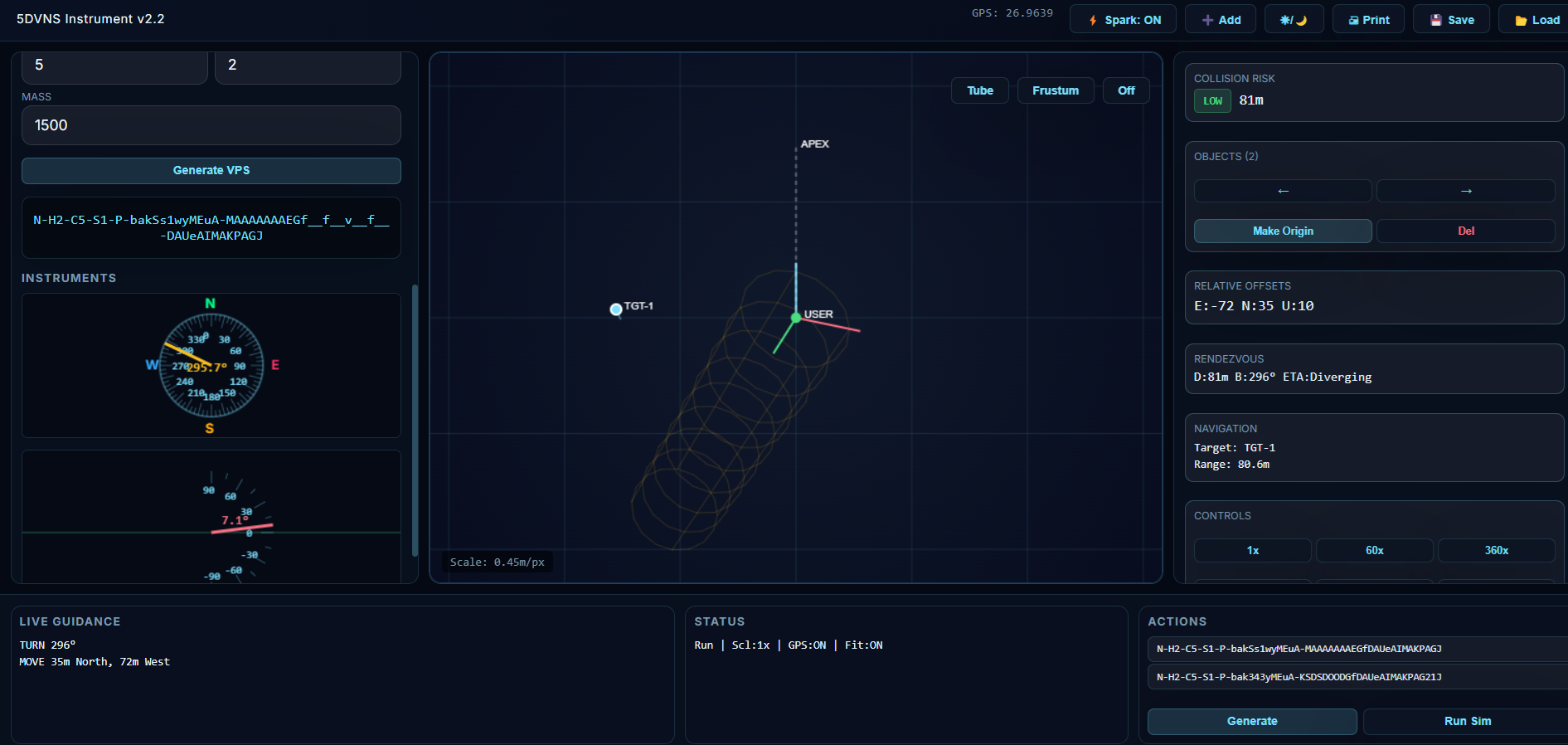
7. Emergent Outputs and Downstream Guidance
All operational outputs in VPS are derived, not prescribed.
Typical emergent outputs include:
- Navigation guidance within constrained volumes
- Corridor and path stability estimation
- Collision, failure, or instability risk metrics
- Decision confidence signals
- Autonomy control primitives
- Forward admissibility projection
These outputs are consequences of state evolution under constraints.
No map, waypoint, or route is required for these outputs to exist.
Guidance emerges when the system detects approaching loss of admissibility.
In this sense:
Guidance is a symptom
Stability is the objective
8. Separation of Integrity and Utility Layers
A defining architectural principle of VPS is the separation between:
- Integrity layers (state admissibility, coherence, bounded uncertainty)
- Utility layers (guidance, visualization, human interfaces)
This separation ensures that:
- The core state logic remains domain-invariant
- Consumer or operator guidance can vary freely
- Visualization does not influence state validity
- Human interpretation is downstream of machine coherence
This makes the framework suitable as a foundational positioning layer, rather than a domain-specific
navigation tool.
9. Applicability Beyond Physical Space
The VPS formalism does not require physical space.
Any system that satisfies the following conditions may be modelled:
- States exist inside bounded constraints
- Transitions occur over time or progression
- Admissibility can be evaluated deterministically
This allows the same formalism to apply to:
- Autonomous agents operating in abstract decision spaces
- Multi-agent coordination under shared constraints
- Graph traversal with viability conditions
- Non-spatial state systems where “position” represents coherence
In such cases, x, y, d need not correspond to physical dimensions.
They represent embedding,
progression, and phase inside a constrained manifold.
This extension is not metaphorical.
It is a direct consequence of the state definition.
10. Summary of the Shift
| Classical Navigation |
VPS / 5DVNS |
| Classical Navigation |
VPS / 5DVNS |
| Point-based |
State-based |
| Coordinate-driven |
Constraint-driven |
| Map-dependent |
Map-agnostic |
| Correction-centric |
Integrity-centric |
| Accuracy-focused |
Confidence-focused |
The VPS framework introduces a structural inversion: position corresponds to a state that remains within
the admissible set over time, not what is measured.
Closing Remark
The VPS framework does not compete with existing navigation systems.
It reframes the layer at which
positioning is defined.
It treats navigation not as the pursuit of coordinates, but as the maintenance of admissible state
evolution.
This makes it a domain-invariant admissibility layer for state-based positioning, autonomy, and reasoning
across domains.
Appendix A — Formal State Definition and Admissibility Model
A.1 State Space
Let the system evolve over continuous time t ∈ ℝ⁺.
Define a bounded manifold ℳ ⊆ ℝⁿ representing the admissible embedding domain.
The Volumetric Positioning State is defined as:
S(t) = (p(t), d(t), V(t))
where
- p(t) ∈ ℳ — lateral embedding
- d(t) ∈ ℝ — scalar progression parameter
- V(t) ∈ 𝒞 — context constraint vector
and 𝒞 is the constraint space.
A.2 Admissible Set
Define the admissible set:
𝒜 ⊆ ℳ × ℝ × 𝒞
A state is valid if:
S(t) ∈ 𝒜
Unlike classical positioning, validity is not defined by proximity to a reference coordinate but by
membership in the admissible set.
A.3 State Evolution
Let system evolution be governed by transition operator:
S(t+Δt) = Φ(S(t), u(t), η(t))
where
- u(t) — control input
- η(t) — bounded disturbance
The VPS condition requires:
Φ(S(t), u(t), η(t)) ∈ 𝒜 ∀ t
Navigation is therefore the maintenance of invariance of 𝒜.
A.4 Bounded Uncertainty
Instead of probabilistic error models, VPS uses bounded uncertainty sets:
η(t) ∈ ℰ(t)
with
ℰ(t) ⊆ ℝᵏ (compact)
Deterministic coherence exists if:
∀ η(t) ∈ ℰ(t), S(t) ∈ 𝒜
Thus position remains defined even under unknown disturbances.
A.5 Loss of Reference Frame
Let R(t) denote an external reference measurement.
Classical navigation requires:
lim ‖p̂(t) − p_R(t)‖ → 0 as t → ∞
VPS removes this requirement.
Instead, coherence requires only:
S(t) ∈ 𝒜 ∀ t
Therefore state validity is independent of the existence of R(t).
A.6 Guidance Emergence
Define admissibility margin:
γ(t) = dist(S(t), ∂𝒜)
Guidance is generated when:
γ(t) → 0
Control actions seek to increase admissibility margin rather than minimize coordinate error.
A.7 Observability Condition
A VPS state is observable if measurements constrain admissible set to a bounded subset:
|𝒜_t| < ∞
Position is therefore defined by constraint convergence rather than coordinate convergence.
A.8 Interpretation
Classical navigation:
Position = estimated coordinate
VPS:
Position = persistent membership in admissible set
Appendix B — Theorems (Statements Only)
Theorem 1 — Admissible State Invariance Under Bounded Disturbance (VPS Coherence)
Setup. Let the VPS state evolve as
S(t+Δt) = Φ(S(t), u(t), η(t))
with bounded disturbance η(t) ∈ ℰ(t), where ℰ(t) is compact for all t. Let 𝒜 ⊆ ℳ × ℝ × 𝒞 denote the
admissible set.
Assumptions.
- Φ is well-defined and continuous in (S, u, η) on the relevant domain.
- For every S ∈ 𝒜, there exists at least one control u ∈ 𝒰(S) such that Φ(S, u, η) ∈ 𝒜 ∀ η ∈ ℰ(t)
(robust admissible successor exists).
Statement. If S(t₀) ∈ 𝒜, then there exists a control policy u(·) such that
S(t) ∈ 𝒜 ∀ t ≥ t₀
i.e., admissibility is a robust forward-invariant property and coherence is preserved without
reference-frame correction.
Interpretation. VPS coherence is the persistence of state membership inside 𝒜 under
bounded disturbance.
Theorem 2 — Reference-Frame Independence of State Validity
Setup. Let R(t) denote any external reference signal (GNSS, map anchor, absolute heading,
etc.). Define VPS validity solely by admissible membership: S(t) ∈ 𝒜.
Assumptions.
- The admissible set 𝒜 and transition map Φ are defined without requiring R(t) as an input for state
definition (reference optional).
- When available, R(t) may refine the constraint vector V(t) but does not redefine 𝒜.
Statement. The truth value of “state is valid” is invariant to the presence or
absence of external reference:
(S(t) ∈ 𝒜) is well-defined even if R(t) ≡ ∅
Therefore, loss of external reference does not imply loss of state definability, only a potential change in
admissibility margin.
Corollary 2.1 (Graceful degradation). When R(t) is removed, coherence can persist as long
as the bounded disturbance set remains compatible with 𝒜.
Theorem 3 — Guidance Emergence From Boundary Proximity (Not Coordinate Error)
Setup. Define an admissibility margin:
γ(t) = dist(S(t), ∂𝒜)
where ∂𝒜 is the boundary of admissibility.
Assumptions.
- 𝒜 is closed and ∂𝒜 is well-defined.
- γ(t) is computable or lower-bounded from the available constraints V(t).
Statement. Any control policy that maintains or increases γ(t) produces navigation
guidance as a byproduct of preserving admissibility:
γ(t) ↓ 0 ⇒ emergent correction signal
and the corrective action is directed toward restoring admissibility (increasing γ), not minimizing
coordinate residuals.
Corollary 3.1 (Collision/risk as admissibility loss). Collision risk, instability risk, or
corridor failure correspond to trajectories that drive γ(t) toward zero.